Learning Threshold Neurons via the “Edge of Stability”

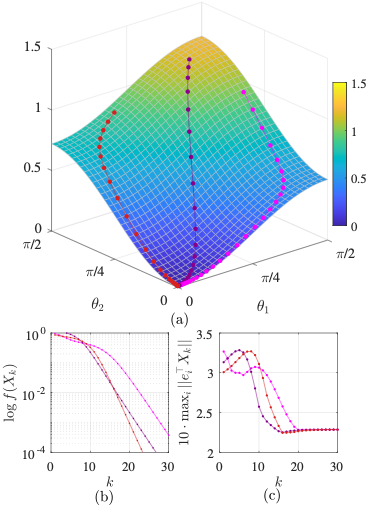
Step sizes beyond the convex optimization threshold can cause gradient descent to diverge. Cohen et al. exhibit a wide class of neural networks where gradient descent self-stabilizes to the size of the step $\eta$, showing that the Hessian stays close to $2/\eta$. This phenomenon is called “edge of stability”.

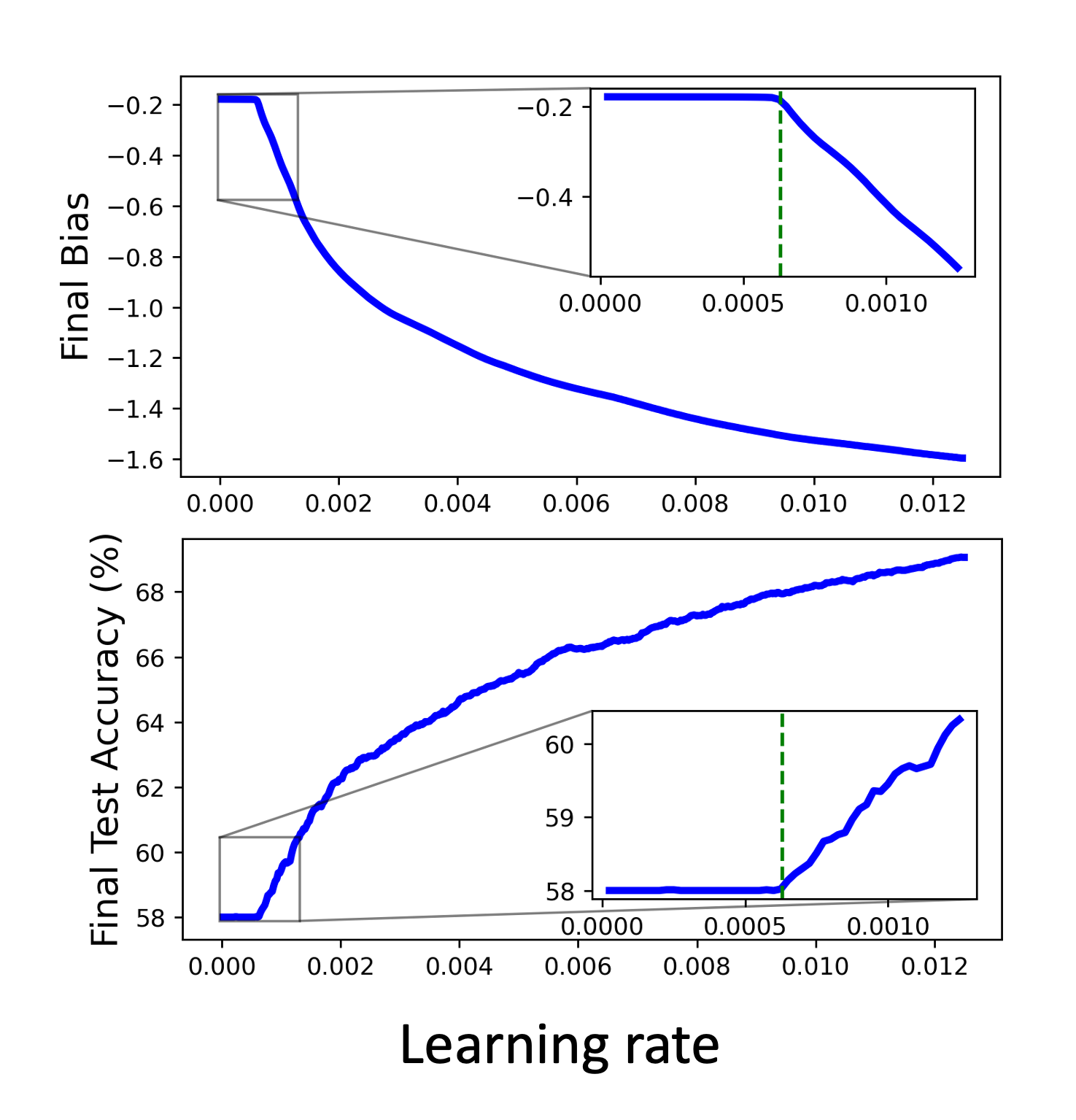
We link the emergence of the “edge of stability” to learning features in neural networks by considering a simple instance of a thresholding problem: the sparse coding problem. We build on the non-convex GD dynamics of a two-variable function $f(x,y) = \ell(xy)$ and characterize the asymptotic limit, Hessian, and convergence times. This analysis also reveals a phase transition in the step size that leads to two regimes: a gradient flow regime and an “edge of stability” regime. For the sparse coding problem, this phase transition carries over to the testing accuracy whereby succesful thresholding is learned via the “edge of stability”.

This is joint work with Kwangjun Ahn, Sinho Chewi, Sébastien Bubeck, Yin Tat lee and Yi Zhang. Check out our paper here.

Wasserstein-Fisher-Rao Splines

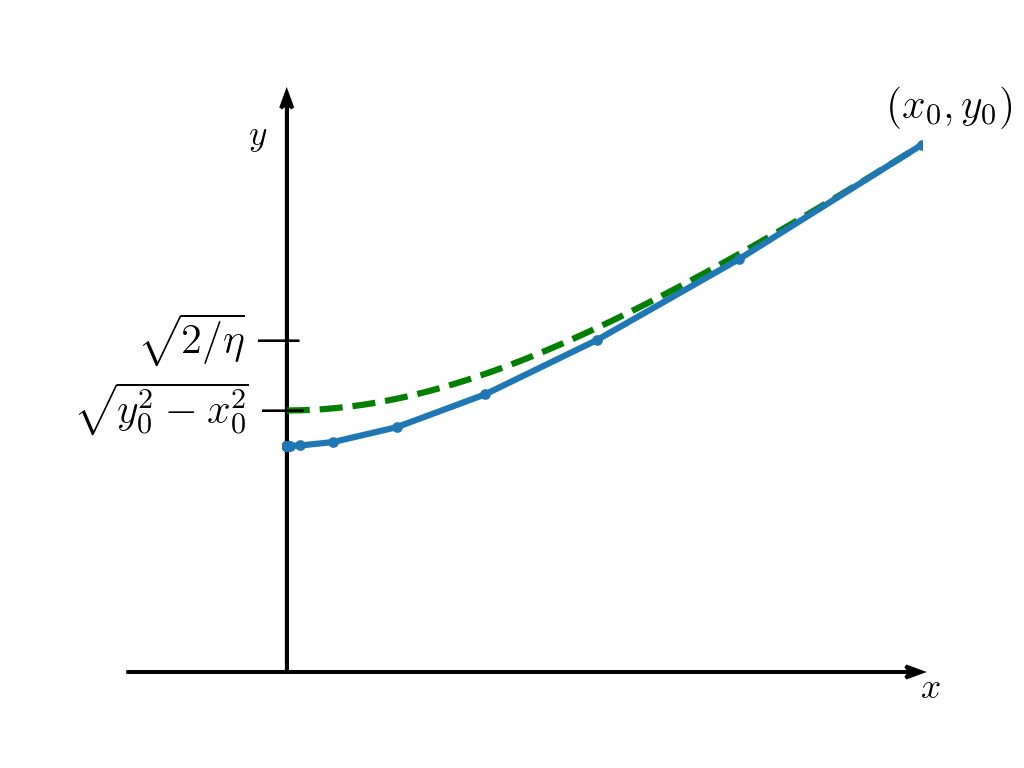
Interpolation is an essential task that seeks to approximate data with smooth curves. In Euclidean space, smooth interpolation can be carried out efficiently via cubic polynomial approximation using Bezier curves, or De Casteljau’s algorithm. Interpolating measures requires dealing with the geometrical properties of measures that is not captured by the flat Euclidean space.

The Wasserstein-Fisher-Rao space offers a geometrically-aware language for dealing with measures. In particular, we exploit the conic lifting of measures and the Eulerian-Lagrangian views on unbalanced optimal transport to approximate curves of measures. Our approach builds on the transport-based approach by Chewi et al. to approximate smooth spline curves via a conic generalization of De Casteljau’s algorithm.

Check out our manuscript here joint work with Julien Clancy.

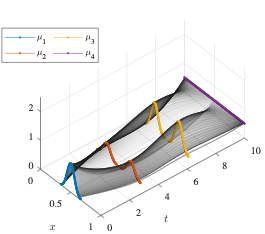
Fisher-Rao geometry and optimization

Linear optimization is a foundational tool applicable in many scientific discplines. Methods for solving LPs come in many flavors ranging from combinatorial and algebraic, to continuous and geometrical. While interior-point methods rely on carefully deregularizing with a self-concordant barrier, entropic methods exploit explicit solutions that lead to efficient mirror map approximations.

Both of these methods can be viewed as gradient flows of a Hessian metric $\langle u,v\rangle_x = \langle u,\nabla^2\phi(x) v\rangle$. IPM is geoemtrized by a Log-metric and entropic methods by the Fisher-Rao metric. In particular, this view leads to simple analyses of convergence rates with implications on algorithmic implementations. We propose methods of approximating these flows building on inexact mirror maps Ballu et al. and mirror-less mirror descent Gunasekar et al.

Riemannian Perspective on Matrix Factorization

Matrix completion has proven succesful as a basic signal processing tool for recovering missing structured data. Framing objectives for completion via factorization over matrices suffers from a clear ill-posedenss: orthogonal rotations leave factorizations unchanged. Building on the works of Rong Ge et al., we show that situation is rather benign.

As a function of subspaces (Grassmannian) rather than matrices, matrix factorization decouples into a simple weighted least squares problem on the (principal) angles of those subspaces. As an immediate consequence, we show no spurious minima exist and convexity holds along orthogonal tangent directions, in particular along normalized gradients.

This is joint work with Kwangjun Ahn in a manuscript here.